微分積分①　～微分とは「変化」を求める方法である～

最近講座ビデオで微分積分を学習してるので、そのメモです。

他人を意識してアウトプットした方が頭の中が整理されることがよ～く分かったので、これからは学習したことをメモ程度でもよいのでブログに書いていこうと思います。
（後からちゃんと記事としてまとめ直すかも）

微積に限らず数学は正直暗記で済ませてきたので、基礎から学習し直しです。
ちなみに、学習に使用しているのは以下の本。

基礎の基礎を説明した本ですが、微分積分のキモがさらりと書かれていてなかなか侮れません。
この本を読んだ後、自分なりに頭の中で整理し直したものをブログに投稿していきたいと思います。

まず、今回は微分とは一体何なのかに関して簡単に説明します！！

微分ものがたり

①「位置」はもう分かった。次に知りたいのは「どう変化するか」だ！！

例えば球を投げると、球の軌道は放物線を描きますよね。物理でもやりました。

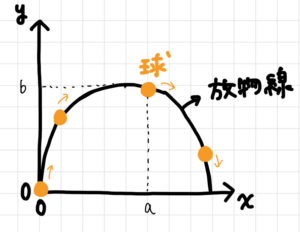
このブラフが表しているのは、

「球の『位置』」

ですね。

このグラフを見れば、球がある位置x=aにあるときにどの高さyにあるのかが分かります（上図ではy=bですね）。

でもこのグラフを見て、

「球がある位置x=aにいる次の瞬間にどう『変化』するのか」

ってすぐに分かりますか？？

正直、戸惑いますよね。

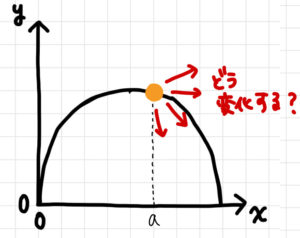
このような、

物の「変化の仕方」を計算するのが「微分法」なのです。

例えるならば、婚活をしているAさんが今B子さんと付き合っている（今のAさんの「位置」に相当）として、今後もB子さんとの仲を深めたいと思っているのか、それともC子さんやD子さんに乗り換えようと企んでいるのか（Aさんのこれからの「変化」に相当）、を考えるようなものでしょうか。

こういう場合、Aさんの両親にとってはAさんが今誰のことを好きかというよりも、最終的に誰と結婚するのかを知りたいはずなので、両親にとってはAさんの「今の位置」よりも「そこからの変化」が重要になってきますよね。

こういうケースで微分が必要になってくるわけです。
（ちょっと強引か？？笑）

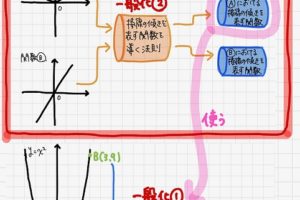
②球の「位置」を表す曲線から球の「変化」を導くことができる！

球の軌道、すなわち球の「位置」を表す曲線があるとします。

この「位置」を表す曲線を用いて、球の「変化」を求めるのが微分法です。

では、具体的にどうやって「変化」を知るのでしょうか。

ここでキモとなるのが、

「変化 = 接線の傾き」

という考え方。

「位置」を表す曲線上の各位置における「接線の傾き」が、その「位置」からの「変化」を示す

と考えるのです。

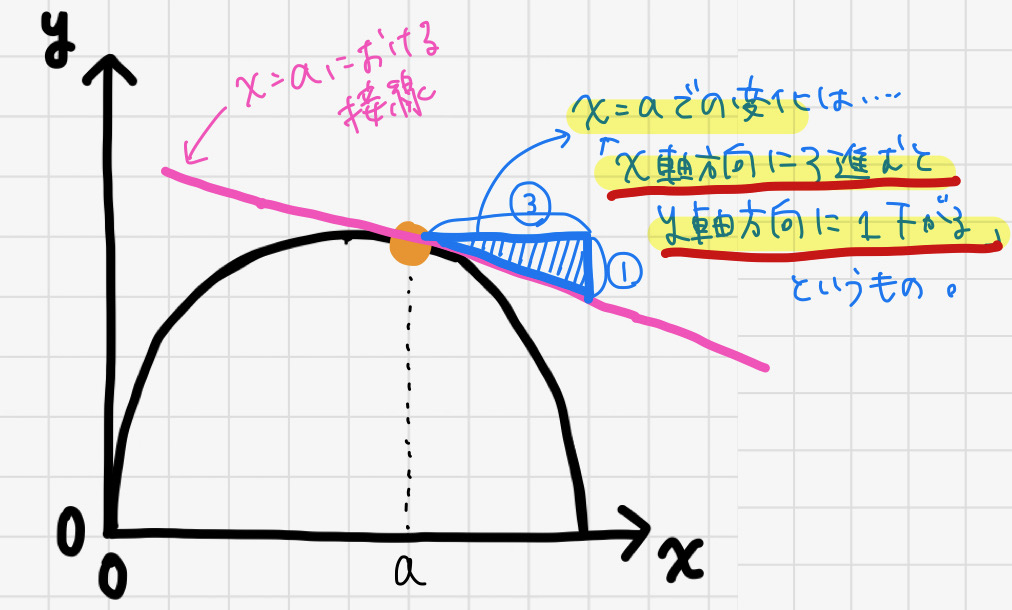
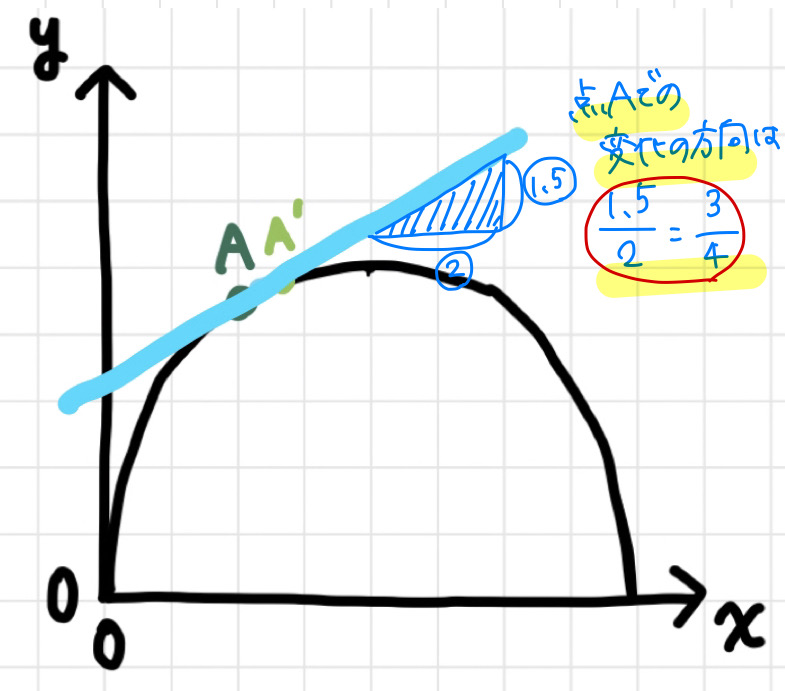
確かに球の場合、「接線の傾き」がその瞬間の進行方向を示すことが直感的に分かると思います。

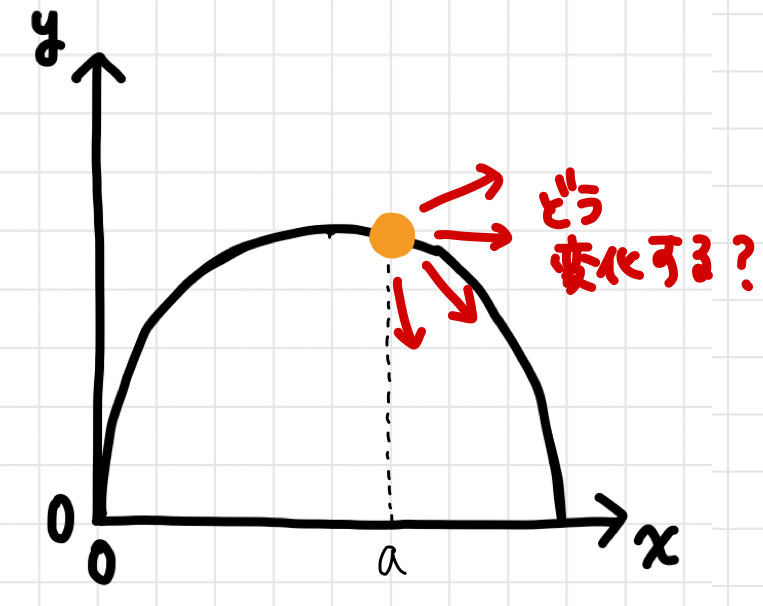
上図だと、x=aにいる球の次の瞬間の変化は、

「x軸方向に3進むとy軸方向に-1下がる方向（つまり傾き-1/3の方向）」

ということになりますね。

③じゃあどうやって接線を求めるの？

では、どうすれば「位置」を示す曲線から「変化」を示す接線を求めることができるのでしょうか。

フリーハンドでなんとなく書けそうな気もしますが、それじゃあ厳密な接線は求めることができませんよね。

どうやって接線を求めるのか。ここの考え方が微分のキモなんですよね～！！（大声）

まず、曲線上のどの位置における変化を知りたいのかを決めましょう。
この点をAとします。

で、その位置とx軸上で少し離れた位置にもう一つ点を取ります。
この点をA’としましょう。

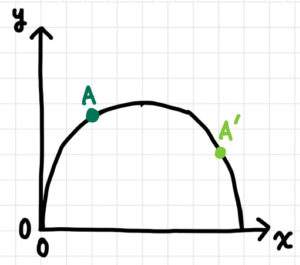
そしてAを動かさずに、A’を曲線上で動かして少しずつAに近づけていきます。

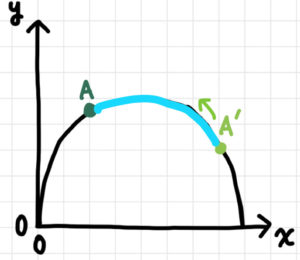
まだ近づける。

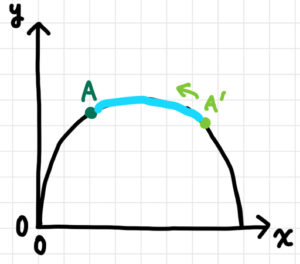
まだまだ・・・。

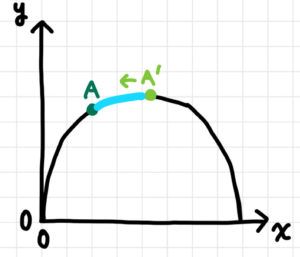
もっと・・・。

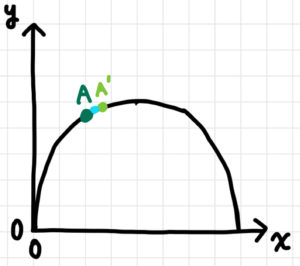
はい、大分近づきました。

次に、点A付近を拡大してみましょう。

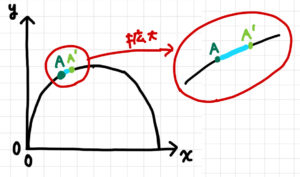
さて、上の図を見て何か気付きませんか？？

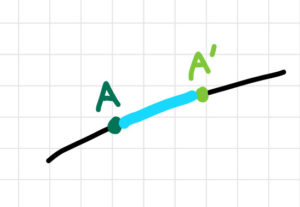
このとき、AA’（曲線上の水色部分）って、曲線じゃなくて直線に見えますよね？？

そして、この直線AA’を引き延ばしてみると・・・

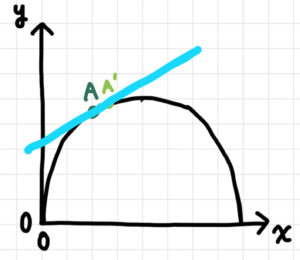
なんと、この直線が点Aでの接線のように見えませんか？？

つまり、

のです！！

この「接線の傾き」が、点Aでの「変化」に相当するんですね。

④接線は直線なので、その傾きも簡単に分かる！（でも少し工夫が必要）

点Aでの「接線の傾き」を求めることで点Aでの「変化」が分かる、というお話をしました。

上の説明では、方眼紙のメモリを元に「接線の傾き」を求めました。

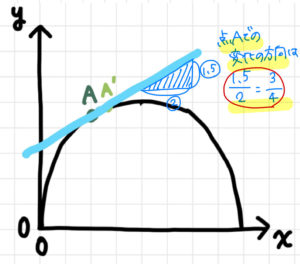
しかし毎回このように方眼紙を使うわけにもいきませんし、何よりx軸方向とy軸方向の変化量が方眼紙のマス目にぴったり一致する場合だけではありませんよね。

ではそのような場合、具体的にどのように「接線の傾き」を計算すればよいでしょうか。

ここで少し工夫が必要となります。
時間の概念を導入するのです。

つまり、

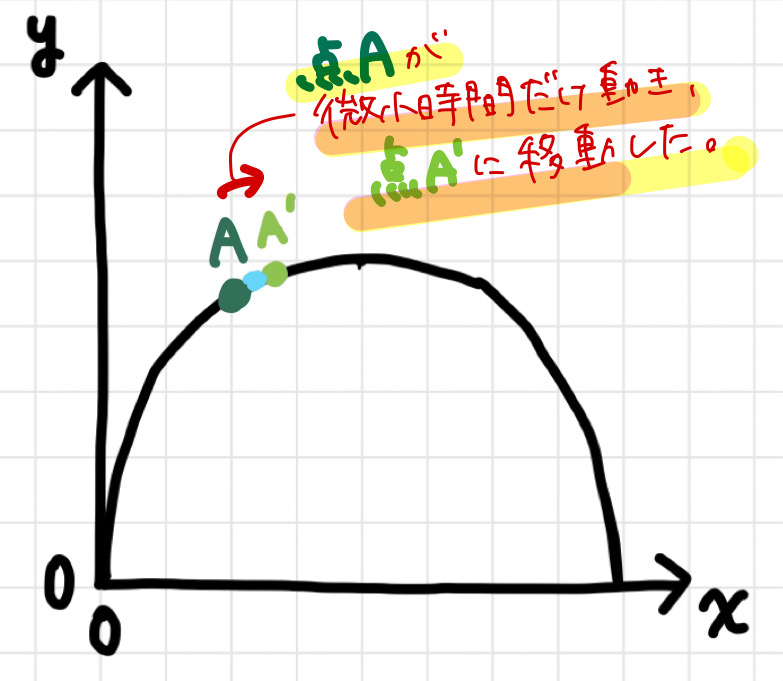
（※ここでは、x=0の点からx軸の正の方向に向かって点が動いていると考えます）

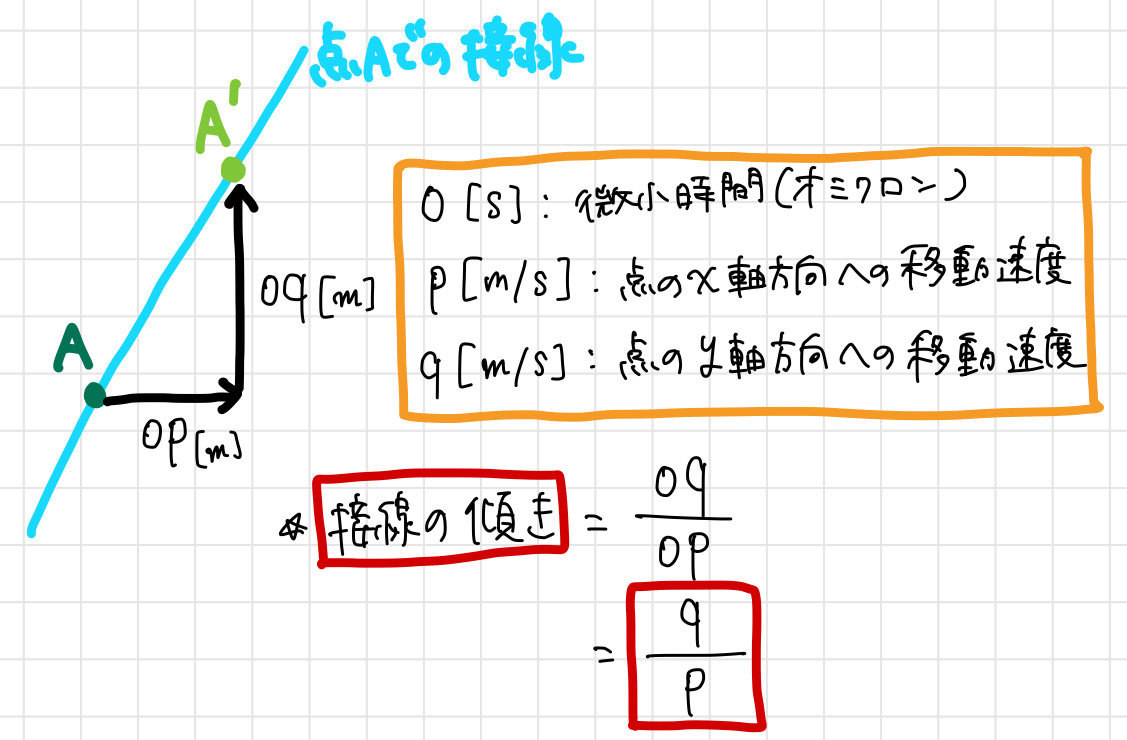
このために導入された記号が、「オミクロン」。

オミクロンは微小時間を表す記号です。
ここでは「o」[s]で表すことにします。

オミクロンを導入し、さらに点のx軸方向の移動速度をp[m/s]、y軸方向の移動速度をq[m/s]とすると、点Aとそれと限りなく近い点A’を通る直線（つまり点Aの接線）の傾きはp/qと表すことができます。

この結果を使用し、例えばy=x^2という二次曲線の点A（2, 4）における接線の傾きを以下のように計算することができます。

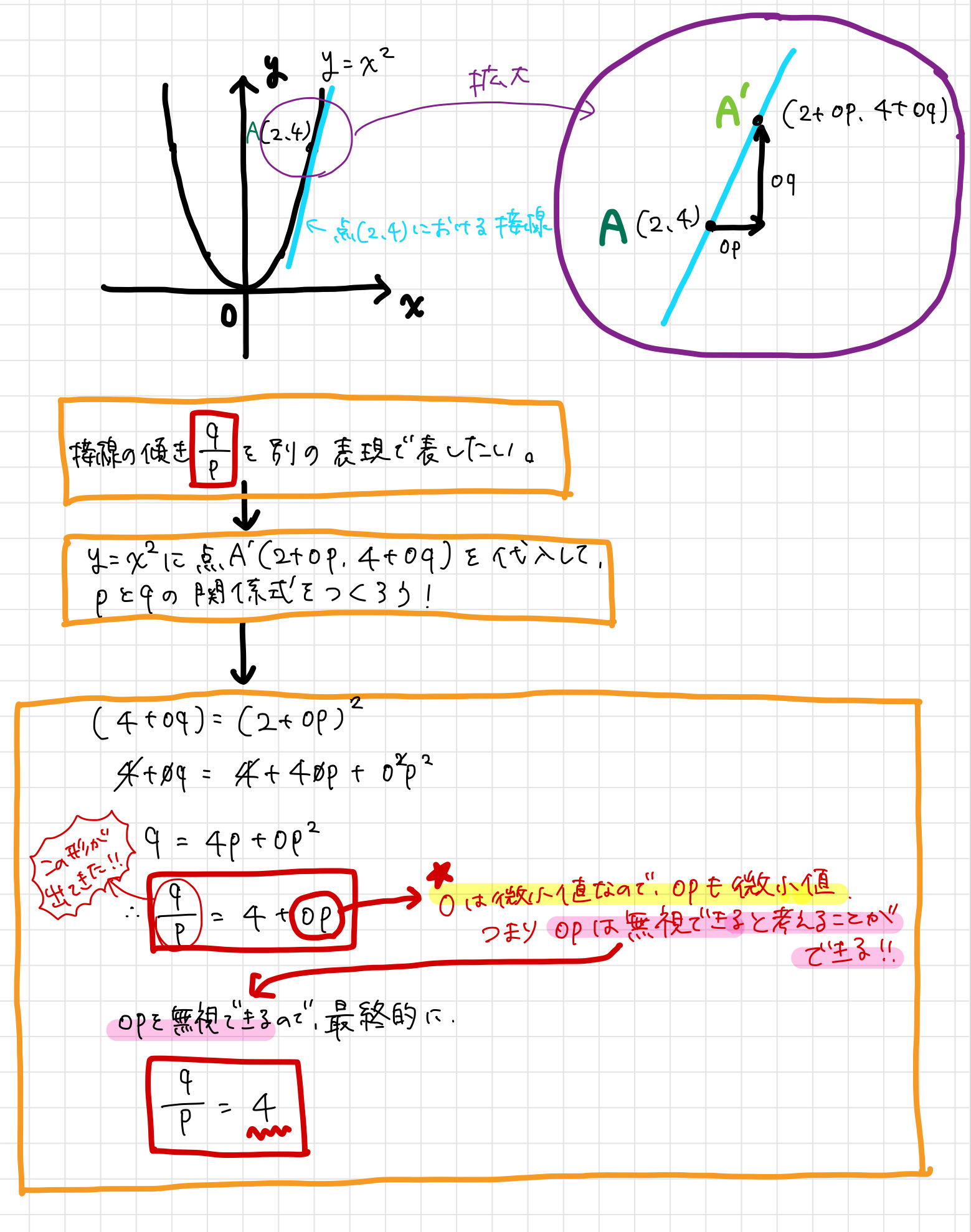
上図でキモとなるのは、「opの値は限りなく小さいので無視できる」と考えた点ですね。

微分ではこのように、

「限りなく近づける」ということを計算において利用するのです。

さあ、これで点Aにおける「接線の傾き」、つまり点Aでの「変化」を求めることができました！

まとめ

微分とは、「位置」の情報を元にその位置での「変化」を求める方法であり、「変化」とはその位置での「接線の傾き」である。

接線は微小時間を考慮することで求めることができ、「接線の傾き」を計算する際にも微小時間という考え方を利用する。

ということを、ざっくりとお話しました。

この、微小時間という考え方の導入が微分の本質であり、革命的なポイントなのですね。

こうやって段階を追っていくと、微分の本質的な考え方を理解することができますね。

そしてやっぱり、考え方を理解できると本当に面白い！！！

今後も数学学習のまとめ、続けていきたいと思います！

参考書籍