さて、前回の記事で微分に興味を持っていただいたそこのあなた。
お待たせいたしました!前回の続きです!!
前回のブログでは、
「微分とは「変化」を求める方法である」
ということを、順を追って説明しました。
前回の最後では、\(y=x^2\)という二次曲線上の点A(2, 4)における接線の傾き、つまり変化を実際に求めてみましたね。
しかし、
点Aの次は別の点B(3, 9)における変化を求めたい、という場合はどうすればよいのでしょう。
また一から接線の傾きを計算し直す必要があるのでしょうか。
いえいえ、数学ではそのようなことはしません。
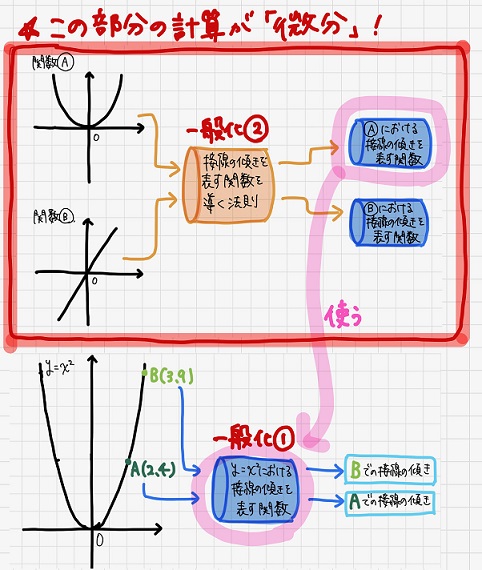
ここで重要なのが、「一般化」という考え方。
「ある関数上」の「任意の点」における接線の傾きを即座に求めることができるよう、ある関数における接線の傾きを表す関数を求めてしまうのです!(一般化①)
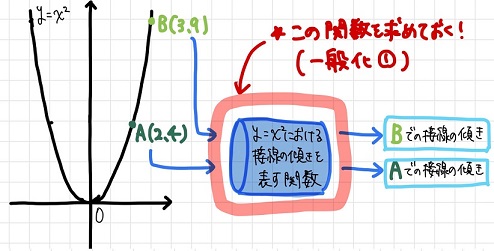
そうすれば、関数上の任意の点の情報をこの関数に代入するだけでその点での接線の傾きを求めることができるようになります。
さらにこの関数の求め方には法則性があり、どのような関数に対しても接線の傾きを表す関数を求めることができます。(一般化②)
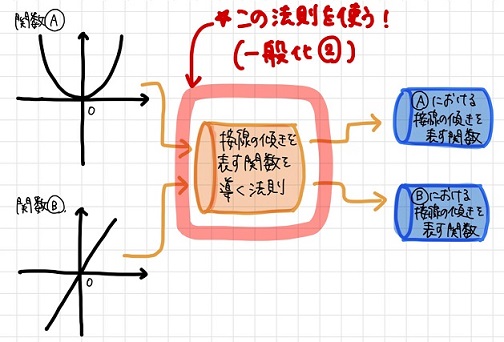
つまり最終的には、
「任意の関数上」の「任意の点」における接線の傾きを即座に求めることができるようになる、
ということですね!
以上の一般化過程をまとめると、以下のようになります。
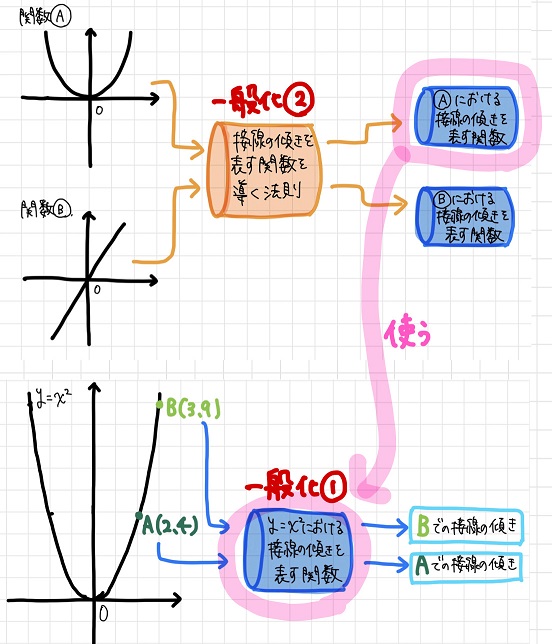
(※この図においては、関数Aは\(y=x^2\)であると考えてください)
それでは、これらの一般化について以下で詳しく説明します!
順番としては「一般化①」の結果を元に「一般化②」の法則性について考えることになるので、まずは「一般化①」から説明しますね。
一般化①:「ある関数上」の「任意の点」における接線の傾きを一般化
まずは、「ある特定の関数上」の「任意の点」における接線の傾きを示す関数を求めてみましょう。

前回のブログと同じく、\(y=x^2\)という関数を使って考えます。
実は、基本的な考え方や計算方法は前回と同じです。
違うのは、\(y=x^2\)上の任意の点を一般化して表すという点です。
例えば\(y=x^2\)上の点Aの任意の\(x\)座標を\(a\)という定数で表しましょう。
この場合、点Aのy座標は\(a^2\)となるため、点Aの座標は\((a, a^2)\)のように表すことができます。

この点\((a, a^2)\)を対象として前回と同じような計算を行うことで、点\((a, a^2)\)における接線の傾きを求めることができます。
具体的な計算を以下に示します。
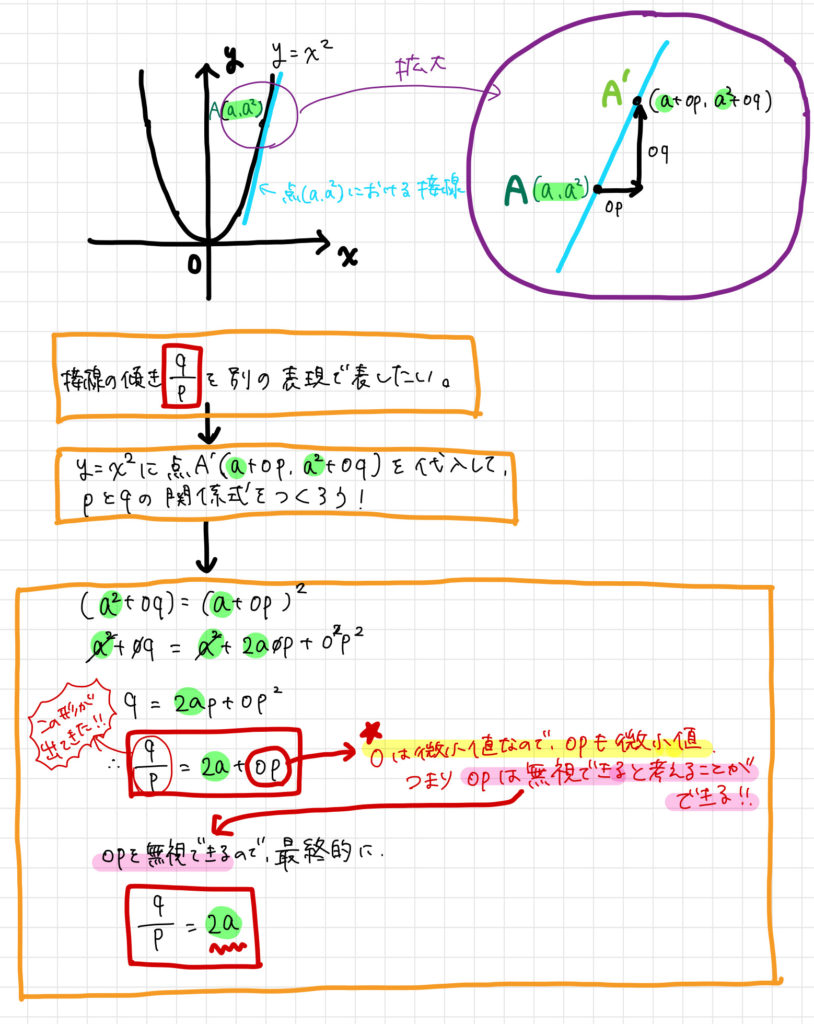
以上の計算により、
\(y=x^2\)上の任意の点\((a, a^2)\)における接線の傾きは\(2a\)である
ことが分かりました。
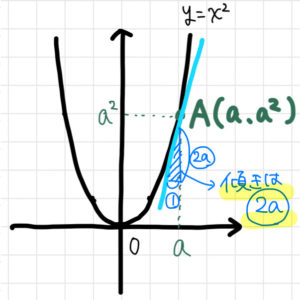
さてさて、ここからが一般化①のキモですよ~。
\(a\)は任意の定数でしたね。
つまり、定数\(a\)は\(x\)軸上の任意の値であると考えられるのです。
イメージとしては以下のような感じでしょうか。\(a\)に\(x\)軸上のどの値を代入してもよいのです。
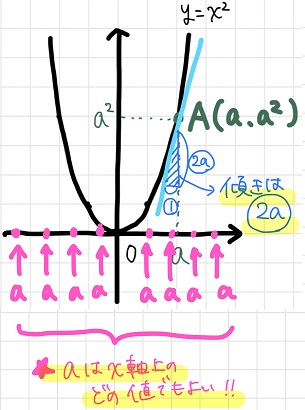
\(a\)にどの\(x\)の値を代入してもよいなら、もう定数\(a\)を変数\(x\)で置き換えてもよくないですか??
そう、よいのです!
そして、
この置き換えこそがまさに一般化①の正体なのです!!
なぜなら、このような置き換えを行うことで、以下の図のように
\(y=x^2\)上の任意の点\((x, x^2)\)における接線の傾きは\(2x\)である
ということになり・・・、
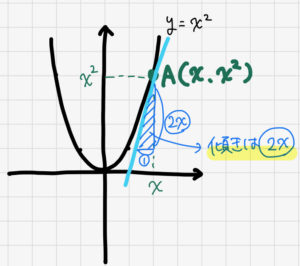
さらにここで、点\((x, x^2)\)における接線の傾きを\(y’\)とすると、
接線の傾きは\(y’=2x\)という関数で表すことができる
ということになるからです。これが一般化①で求めたかった関数なのです!!
このような接線の傾きを表す関数は、元の関数の「導関数」と呼ばれます。
両者のグラフを並べて描くと、その関係が理解できるかと思います。
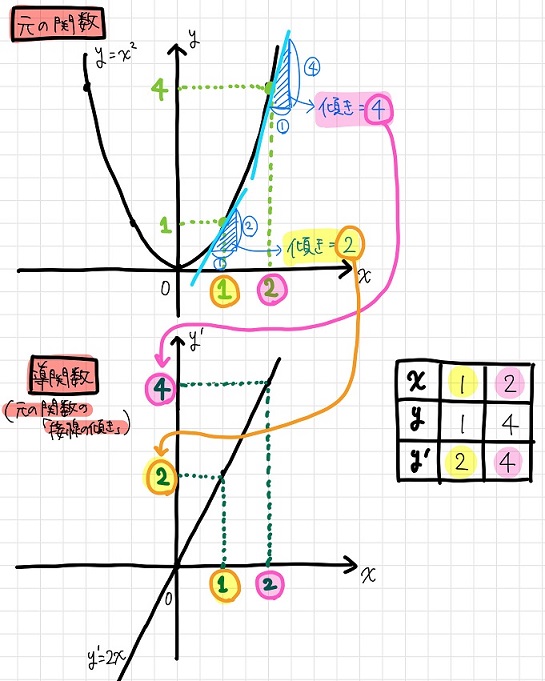
さてこれで、導関数\(y’=2x\)を用いて\(y=x^2\)における任意の点の接線の傾きを求めることができるようになりました!
一般化②:「任意の関数上」の「任意の点」における接線の傾きを一般化
一般化①では、\(y=x^2\)という「特定の関数」における接線の傾きを表す関数(導関数)を求めました。
次に、一般化①の計算結果を用いて
「任意の関数」における導関数を求めるための法則
を考えましょう。

元の関数とその導関数との関係性について考える
様々な関数に関して一般化①のように考えると、元の関数とその導関数との間には以下のような関係性があることが分かります。
元の関数:\(y=x\) → 導関数:\(y’=1\)
元の関数:\(y=x^2\) → 導関数:\(y’=2x\)
元の関数:\(y=x^3\) → 導関数:\(y’=3x^2\)
(※\(y=x^2\)に関しては上の章で説明しましたね。\(y=x\)と\(y=x^3\)のケースに関しても、上の章を参考にしてぜひ自分で考えてみてください!)
上記の関係性をよく見ると、
導関数では元の関数の指数部分の数字がxの前に出てきて、指数部分の数字が1小さくなっている
ことが分かります。
つまり、以下のような法則性があるということですね。
(※今回は\(n\)が整数であるケースしか議論してませんが、実は\(n\)は任意の実数とすることができることが証明されています)
この法則性は、いわば導関数を求めるための公式です。
この公式を用いれば、元の関数から簡単にその導関数を求めることができます!
これが一般化②の正体です!
このように、具体例からその法則性を見つけ出して一般化することで、導関数を求めるための公式を得ることができるのですね。
そして、このように元の関数からその導関数を求める計算こそがまさに「微分」なのです!!
(※この図においては、関数Aは\(y=x^2\)であると考えてください)
\(y=ax^n\)
(\(a, n\)は整数)
であるケースに限定して説明しています。
実際はこのような形以外の任意の関数に関しても微分の公式が存在し、その導関数を求めることができます。
まとめ
今回は、微分の「一般化」に関して説明しました。
一般化することで、「任意の関数上」の「任意の点」における「接線の傾き」、つまり「変化」を求めることができるんですね。
微分は、「変化」を分析することが必要となる様々な場面で大いに活用されています。
微分の考え方をマスターすれば、世の中の見方も変わってくるのではないかと思います。
さて、次回はとうとう積分のお話に入ります!!
微分とは切り離せない積分・・・。
積分に関しても私は曖昧にしか理解してこなかったので、この機会にしっかりと基礎を押さえたいと思います!
参考書籍
↓上の本の内容がもう少し詳しく説明されてます。図解が豊富で分かりやすい!コラムも面白いです。


コメントを残す