さあ、今回も微分積分の世界への旅を始めましょう!!
前回までは、微分の考え方とその一般化について解説しました。
今回は、いよいよ積分の話に入ります!
当初は微分とは全く別のものであると考えられていた積分ですが、その後、両者の間には切っても切れないふか~い関係があることが分かります。
つまり、微分と積分を両方理解して初めてその体系を知ることができる、ってことですね。
今回はまず、積分の基本的な考え方について、その歴史と絡めながら説明していきます!
積分の考え方:「無限に小さくして足し合わせる」!
「無限に小さくして足し合わせる」
積分の考え方を一言で表すなら、これです。
面積や体積を求めるのが困難な領域を計算可能な無限に小さい領域に分割して、それらを足し合わせることで対象領域全体の面積や体積を求める
のです!
一般的には、直線で囲まれた領域の面積は簡単に求められそうですが、曲線で囲まれた領域の面積を求めるのは難しそうですよね。
こういう場合に、曲線で囲まれた領域を直線で囲まれた微小な領域に分けて、それら各々の領域の面積を足し合わせることで曲線で囲まれた領域の面積を求めるのです!
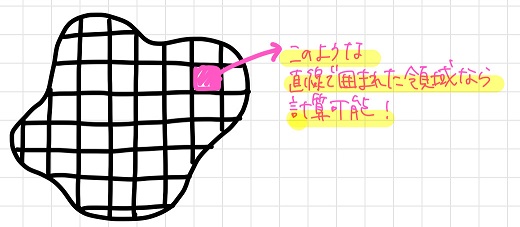
もちろん誤差が出ますが、領域の分割数を大きくすることで誤差を小さくすることができます。
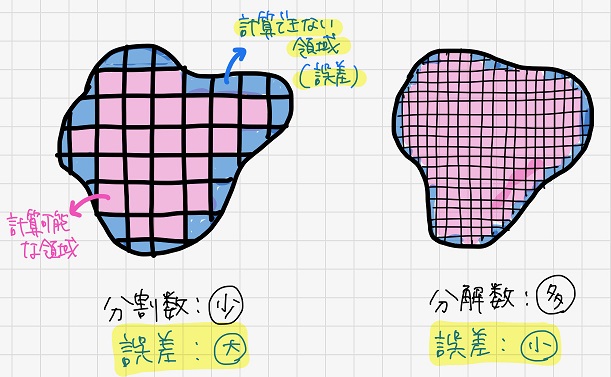
そして、ここで「無限」というワードが出てきましたね。このワード、微分のときも出てきました。
(微分における無限は、「関数上の2点を『無限』に近づけて接線を求める」というものでしたね)
微分と積分には、「無限」という共通のキーワードがあるんですね。この事実からも、微分と積分の間のふか~い関係がほのめかされますね。
積分は、複雑なものを簡単なものに分けて理解することに似ている
例えば、複雑で訳が分からない内容の書類があるとします。
でもその内容をいくつかの節に分けて、その節毎に内容を理解していけばいつかは書類の内容全体を理解できるはずですよね。
積分は、これと似ていると思います。
複雑なものを簡単なものに分けて理解し、それを後で組み合わせる。
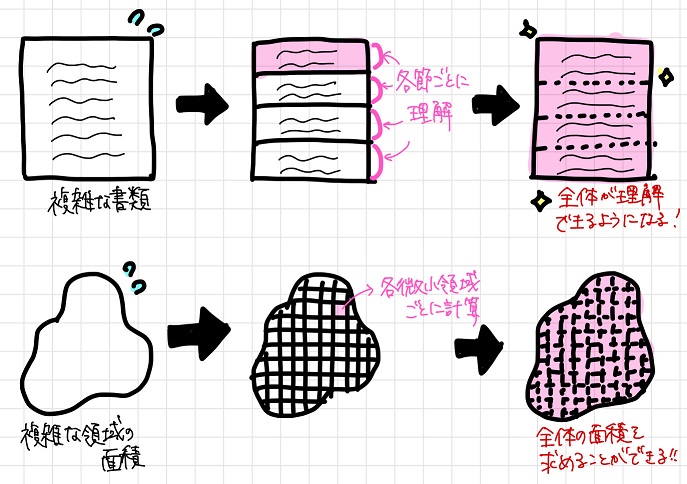
このような工程を経ることで、どんなものに関しても(誤差はあるでしょうが)ある程度理解できると思います。
こう考えると、積分法は複雑な世の中を理解するための重要な方法であると言えそうですね。
積分はどう発展してきたのか?積分の歴史を覗いてみよう!
微分と積分とのふか~い関係を発見したのはニュートンですが、そこに至るまでは先人たちの様々な努力がありました。
これら先人たちは、
「無限に小さくして足し合わせる」
という「微分の考え方」を用いて様々な領域の面積、体積を求めようと努力してきました。
ここでは、彼らの業績を時系列順に少し見てみようと思います。
実例を見ることで、積分の考え方にだんだん慣れてくると思いますよ!
①アルキメデス:取りつくし法
まずは古代ギリシアの数学&物理学者、アルキメデスによる「取りつくし法」です。
これは、放物線と直線に囲まれた領域の面積を求める方法です。
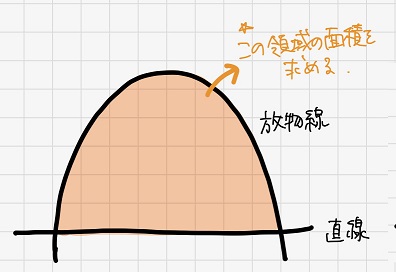
彼はこの領域を無数の三角形で分割することで、この領域の面積を求めました。
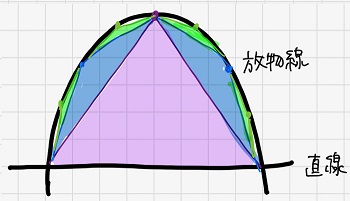
常に面積が最大となるような三角形をつくるようにして、領域の残りの隙間を埋めていきます。
(上図中では、紫の三角形、青の三角形、緑の三角形・・・の順で領域を埋めていっています)
そうすると、やがては無限に小さな三角形で隙間がほぼ埋められることになりますよね(もちろん誤差はありますが)。
各三角形の面積は簡単に求められるので、対象領域を分割した三角形の面積を全て足すことで対象領域の面積を求めることができるのです。
②ケプラー:扇形の面積(ケプラーの第二法則)&ワイン樽の体積
次は、アルキメデスからなんと一気に1800年ほどジャンプした16、17世紀。ケプラーによる方法です。
ケプラーは天文学者であり、火星の軌道を正確に計算する方法について試行錯誤していました。
この試行錯誤の過程で、彼は
「一定時間に、太陽と火星を結ぶ直線が通る扇形の面積」
を求める必要に駆られます。
この扇形の面積を求める際に「積分の考え方」を利用したのです!
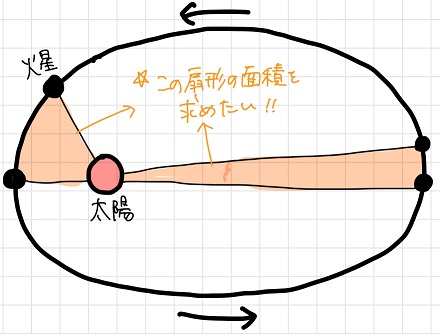
具体的には、アルキメデスによる取りつくし法のように扇形領域を無限に小さな三角形に分けて計算したようです。
具体的にどんな風に三角形に分けたのか、詳しい資料は見つからなかったのですが、取りつくし法を参考に推測すると以下のような感じでしょうか・・・。

そしてこの結果が、
「一定時間に、太陽と火星を結ぶ直線が通る扇形の面積は等しい」
というケプラーの第二法則に繋がっていくのです。
またケプラーは、「積分の考え方」を用いてワイン樽の体積を求める方法も提唱しています。
ワイン樽。私も実物を見たことはありませんが、これです。

この樽、弓のようにしなった形をしているので体積を求めるのが難しそうですよね。
そこでケプラーは、この樽を横方向に無限に小さく分割し、無限に薄い円盤の集まりであると見なしました。

各円盤の体積は簡単に求められますよね。
そのため、各円盤の体積を計算してそれらを足し合わせることで、ワイン樽全体の体積を求めることができるのです!
これはまさに、「無限に小さくして足し合わせる」という積分の考え方そのものですね!
(ケプラーがワイン樽の体積を求めることになったいきさつに関してはこちらのページが詳しいです。新たな発見の種って、身近なところに転がっているものなんですね~。)
③カヴァリエリ:カヴァリエリの原理
お次はケプラーと同じく17世紀。ガリレオの弟子であるカヴァリエリによるものです。
カヴァリエリはケプラーがワイン樽を求めた方法にヒントを得て、面積や体積を求めるための新しい考え方を提唱しました。
例えば、以下のような複雑な領域の面積を求めたいとしますよね。
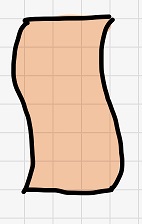
この領域、側面が曲線になっていて面積を求めるのはなかなか難しそうです・・・。
どうしたものか・・・ということで、この領域を、ケプラーのワイン樽のように横方向に小さく分割してみます。
すると、以下のように長方形を縦に重ねたものと考えることができますよね。
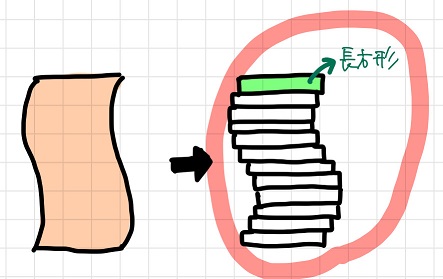
そして、各長方形を縦に揃えると・・・。
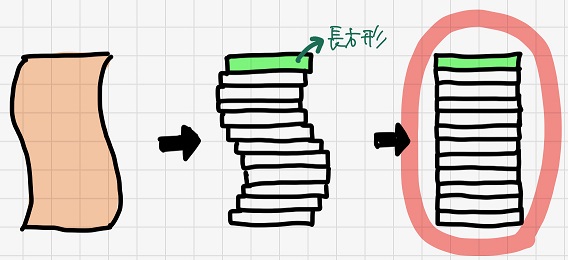
なんと、領域全体が長方形に変化しますね!!
つまり、この長方形の面積が最初の複雑な領域の面積と等しい、と考えられるのです!
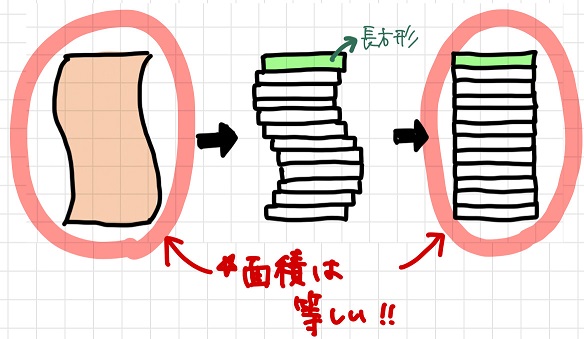
この長方形の面積が分かれば、それとの「比較」として最初の複雑な領域の面積を求めることができるということですね!
この事実は以下のように、「カヴァリエリの原理」として一般化できます。
先ほどの例の場合、スライス片を横にスライドしただけなのでもちろん各スライス片の幅は変化しません。そのため、カヴァリエリの原理が成立するんですね。
より複雑な図形に関しても同様です。
例えば、以下の2つの領域の面積は同じです。両領域のスライス片の幅を比較すれば分かりますよね。
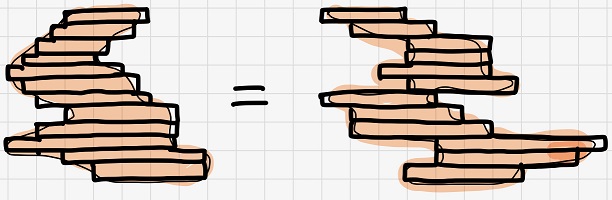
ちなみに上の定義中、「幅」を「面積」、「図形」を「立体」と読み替えれば、「カヴァリエリの原理」は立体に関しても成立します。
立体に関しては、以下の写真を見るとイメージがわくかと思います。

(出典:Wikipedia「カヴァリエリの原理」)
どんな領域に対しても適用できる一般的な方法は出てこなかった
さて、上で見てきた3人の先人たちによる様々な方法を以下にまとめてみました。

さて、上の表を見て何か気付きませんでしょうか??
・・・そうなのです。
これらの方法、どんな領域に対しても適用できるわけではないのです!!
表中の「面積or体積を求めることができるもの」に記載されているものに対してしか適用できないんですね。
カヴァリエリの原理に関しては、2つの領域の面積or体積が等しいという比較自体はどんな場合にも可能でしょうが、その面積or体積を求めるのは難しいこともありそうです(長方形のような単純なものなら可能でしょうが)。
どんな領域に対しても適用できるよう、積分の考え方を一般化する必要がありますね。
さて、どうしましょう。
そしてニュートンへ・・・
その後積分の考え方を一般化したのは、微分の説明でも幾度となく登場したニュートンでした!
ニュートンは積分の考え方を一般化し、さらに微分と積分とのふか~い関係も発見してしまいます。
そしてこれが、微分と積分との統一につながるのです!!
まとめ
今回は、
「無限に小さくして足し合わせる」
という積分の考え方に関して、先人たちによる例を挙げながら説明しました。
先人たちにより様々な方法が発見されましたが、どれも積分の考え方を一般化できるものではありませんでしたね。
次回は、
ニュートンによりどのように積分の考え方が一般化されたのか、
そして
そこからどのように微分と積分が統一されたのか、
について説明したいと思います!
参考書籍
↓上の本の内容がもう少し詳しく説明されてます。図解が豊富で分かりやすい!コラムも面白いです。



コメントを残す