さて、微分積分の話も佳境ですね!!
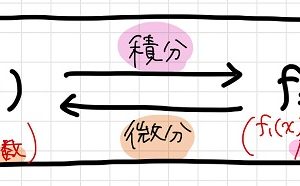
前回は微分と積分との間のふか~い関係、つまり、
「微分と積分は逆の関係にある」
ということについて説明しました。
この関係が発見されたことで、様々な領域の面積や体積を求めることが可能になったんでしたね!
まさに革命的な発見だったわけです。
↓前回の記事はこちら!↓
そして今回は、前回のブログでちらっと出てきた2種類の積分方法、
「不定積分」と「定積分」
に関して詳しく解説します!
これらの違いや特徴、関係性について知ることで、積分に対する理解が格段に深まることでしょう。
また、これらを考える際には、
「積分定数」
というものを理解する必要があります。
「不定積分」と「定積分」、そして「積分定数」。
これらの関係性はどんなものなのか?早速見ていきましょう!!
不定積分と定積分の違い・関係性は??
「不定積分」と「定積分」との違いは一体何なのか。一言で言えば、これらは
「求める対象が違う」
のです。
「不定積分」が求める対象は「面積を表す関数」
であり、
「定積分」が求める対象は「ある領域の面積自体」
なのです!
そして実は、これらの間には、
定積分で面積を求めるときには不定積分で求めた関数を使う
という関係性があるのです!!
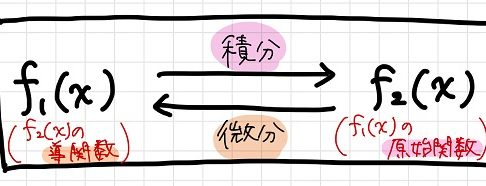
この関係性を図で表すと、以下のようになります。
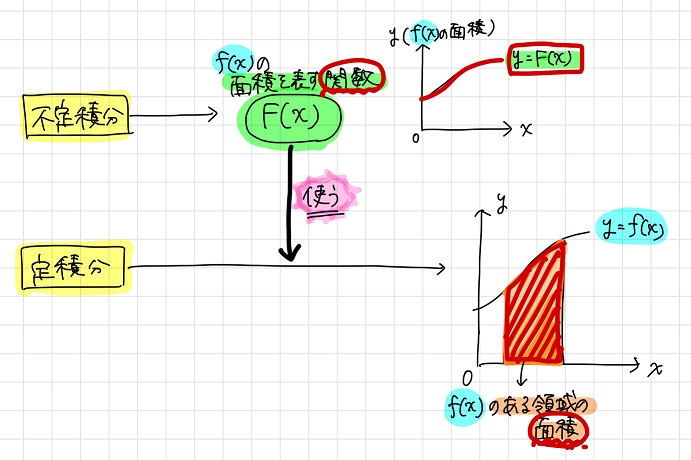
具体例:不定積分と定積分を使ってある関数の特定領域の面積を求めるまで
例えば、関数\(y=x\)の\(1≦x≦2\)の領域における面積を求めることを考えましょう。
これは「ある領域の面積自体」を求めることなので、「定積分」ですね。
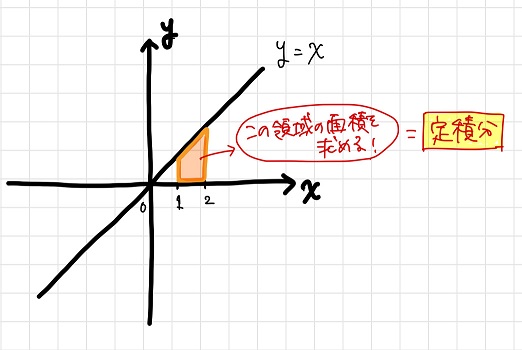
さて、では
どうやってこの領域の面積を求めましょうか?つまり、どうやって定積分したらよいでしょうか?
このときに、不定積分の結果を使うのです!
①まずは不定積分する
不定積分については、実は、前回のブログ内の
『「ある関数を積分して、その関数の面積を表す関数を得る」とは?』
にて説明しています。
元の関数からその原始関数を求める操作が「不定積分」なんですね。
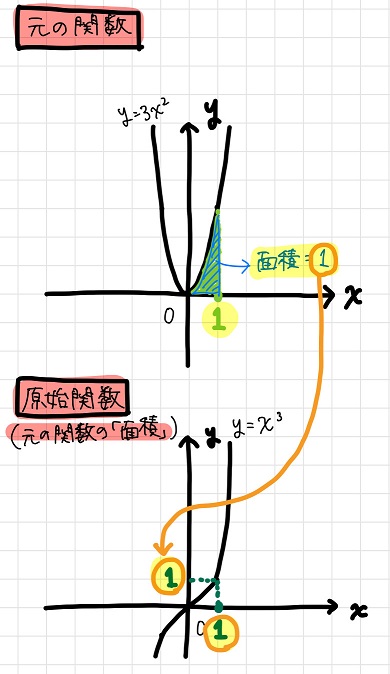
(※前回のブログより、元の関数が\(y=3x^2\)である場合の例を再度掲載。)
~~~~~
最初に、不定積分により\(y=x\)の面積を表す原始関数を求めておきます。
前回のブログで説明したように「微分と積分は逆の関係にある」ので、微分の逆の計算をすれば原始関数を求めることができますね。
今回の場合、原始関数は\(y= \frac{1}{2}x^2\)となります。
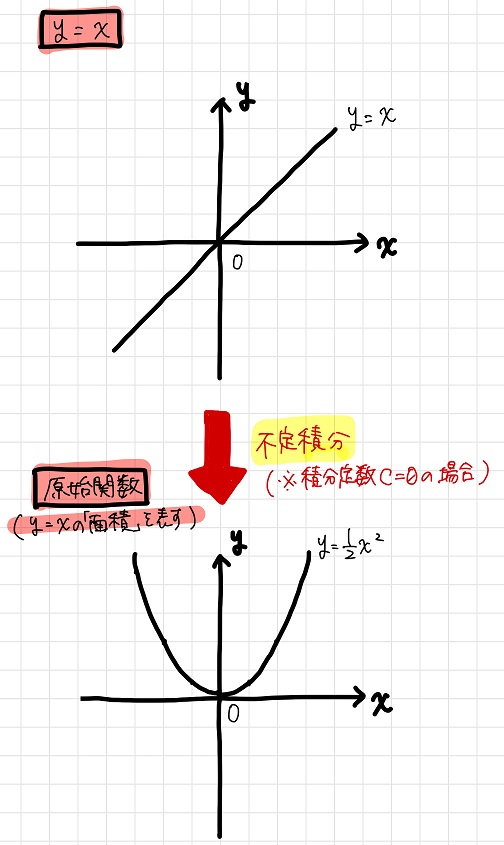
ここでは不定積分と定積分との関係性を考えやすくするため、積分定数が0であると仮定して説明しています。
(実は前回のブログでも、積分定数が0であるとして説明していました)
積分定数が0ではない場合に関しては、後ほど説明します!!
②不定積分で求めた原始関数を使って定積分する
前回のブログで示した原始関数の定義から考えると、
原始関数\(y= \frac{1}{2}x^2\)に
\(x=1\)を代入した結果が\(y=x\)の\(0≦x≦1\)の領域の面積であり、
\(x=2\)を代入した結果が\(y=x\)の\(0≦x≦2\)の領域の面積です。
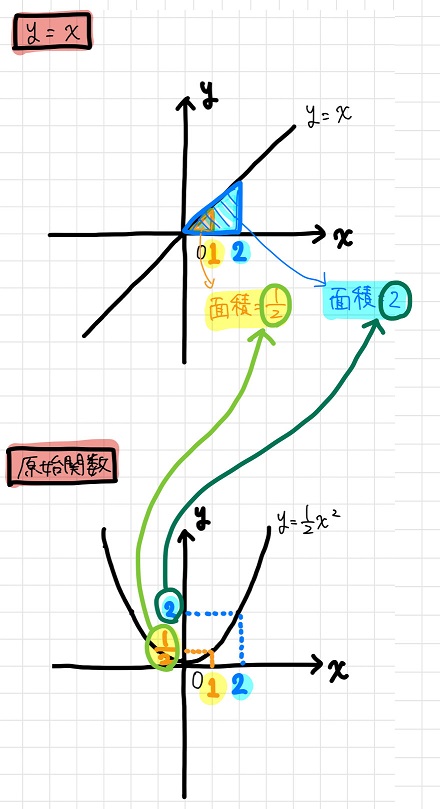
つまり、\(y=x\)の\(1≦x≦2\)の領域の面積は、
原始関数\(y= \frac{1}{2}x^2\)に\(x=2\)を代入した結果から\(x=1\)を代入した結果を引いたもの
となるんですね!
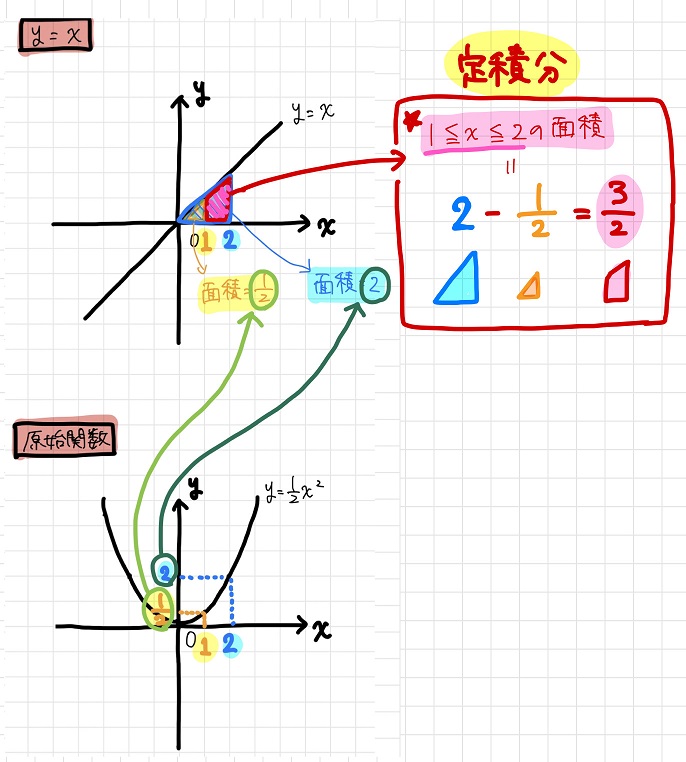
そして、実はこの
「原始関数に面積を求めたい領域両端のxの値を代入して差し引く操作」こそが定積分そのもの
なのです!!
不定積分と定積分には、このような関係性があったんですね!!
積分定数とは?
さて、それではここで、これまで無視してきた(笑)
「積分定数」
というものについて解説します!
積分定数とは、一体何者なのでしょうか??
積分定数 = 不定積分すると出現するもの
実は、積分定数は不定積分した際に原始関数の一部として出現するのです!
例えば\(y=x\)を不定積分すると、その原始関数は以下のようになります。式中の\(C\)が積分定数です。
「あれ?さっき\(y=x\)の面積を求める際に不定積分したときには原始関数は\(y= \frac{1}{2}x^2\)だって言ってたじゃん。積分定数なんて出てこなかったけど??」
というそこのアナタ。するどいです。
そう、実は、先ほどの計算は、積分定数\(C=0\)であるとした場合の計算だったんです!!
なぜ先ほどの計算では、積分定数\(C=0\)としても大丈夫だったのでしょうか??
これに関しては、後ほど詳しく説明します。
その前に、積分定数とは一体何のために付けるものなのか、つまり積分定数の正体について説明したいと思います。
積分定数を付ける理由とは?
積分定数。それは、
「元の関数の原始関数が無数に存在するため、その原始関数全てを表現するために付けるもの」
なのです!
つまり、積分定数\(C\)にどんな定数が入ったとしても、その全てが元の関数の原始関数となるんですね。
原始関数を一つに決められないので、未確定の定数として積分定数\(C\)を付けておくのです。
(ちなみに、積分定数\(C\)は実数です)
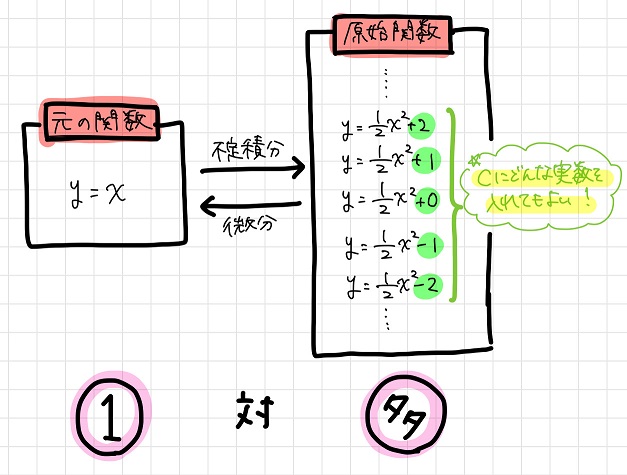
では、なぜ元の関数の原始関数は無数に存在するのでしょうか?
それは、微分の意味を考えるとよく分かります。
元の関数と原始関数との関係を考える
例えば、\(y=x\)という関数を不定積分して原始関数を求めることを考えてみましょう。
先ほど述べたように、
です。
ここで、積分定数\(C\)を様々に変化させた原始関数をいくつか挙げてみましょう。
\(C=2\)の場合:\(y= \frac{1}{2}x^2 + 2\)
\(C=-3\)の場合:\(y= \frac{1}{2}x^2 – 3\)
次に、これら3つの原始関数\(y= \frac{1}{2}x^2\)、\(y= \frac{1}{2}x^2 + 2\)、\(y= \frac{1}{2}x^2 – 3\)を比較してみましょう。
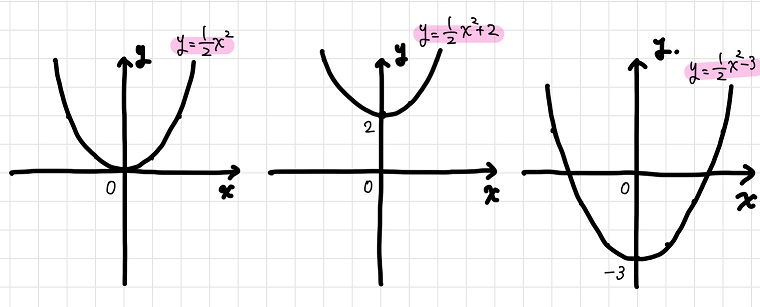
これらの違い、何だか分かりますか??
・・・そう。これらは、どれも\(y= \frac{1}{2}x^2\)という関数をy軸に沿って平行移動させたものなのです!
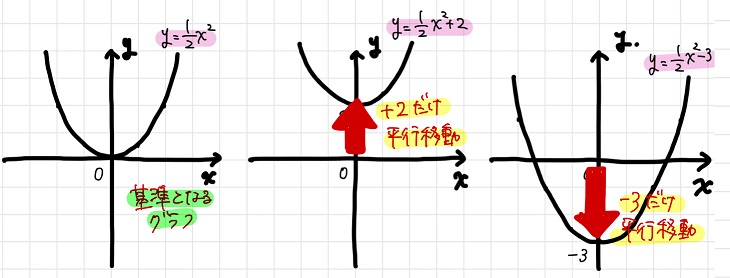
\(y\)軸に沿って平行移動させただけなので、これら各原始関数の接線の傾きはもちろん全て同じです。
つまり、これら各原始関数の導関数は全て\(y=x\)になるんですね。
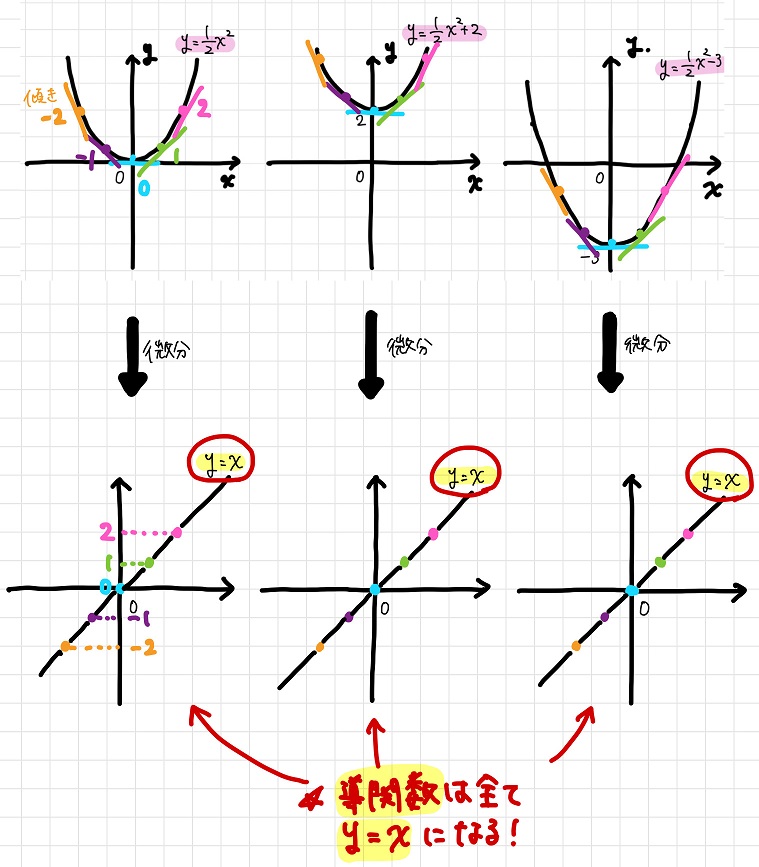
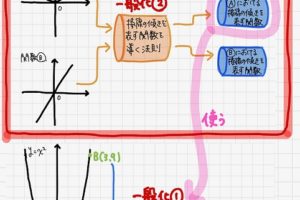
以上を一般化すると、元の関数と原始関数との間には以下のような1対多の関係があるということになります。
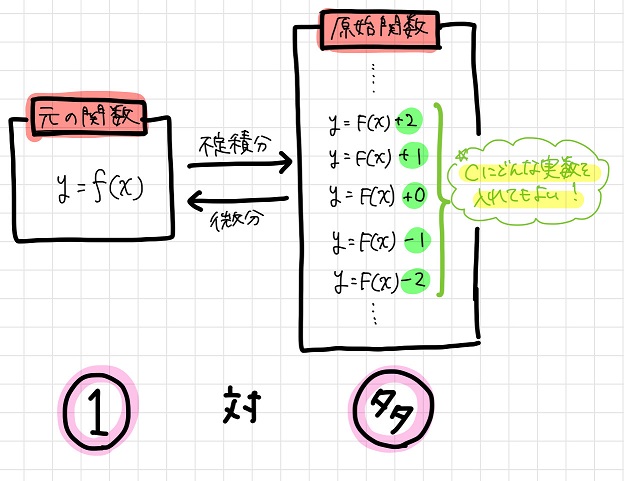
ある元の関数に対して、その原始関数は多数存在する。
この「多」の部分を表すために、原始関数には積分定数が付いているんですね!
疑問:なぜ積分定数\(C=0\)として定積分しても問題ないの??
さて、お待たせいたしました。
長々と引き延ばしてきましたが、
「原始関数には積分定数Cが含まれるって言うのなら、何でさっきは積分定数\(C=0\)として定積分したの??」
という疑問にお答えしたいと思います!
ここの理屈を抑えておけば、定積分に関する理解が深まること間違いナシですよ!!
回答:積分定数\(C\)の値は、定積分の結果に影響しないから!
そうなのです。
実は、
「積分定数\(C\)の値は、定積分の結果に影響しない」
のです!!
定積分は原始関数を用いて行うものですが、原始関数に含まれる積分定数\(C\)がどんな値であっても定積分の結果は同じになるんです!
そのため、先ほどは積分定数\(C=0\)として計算したんですね。
では、なぜ積分定数\(C\)がどんな値であっても定積分の結果は同じになるのでしょうか??
実際に積分定数\(C\)を様々な値に設定して定積分を実行した上で、その理由を検討してみましょう!
検討:積分定数\(C=0\)の場合
元の関数を\(y=x\)、定積分の範囲を\(a≦x≦b\)(\(0<a<b\))として検討します。
まずは先ほども少し述べた、積分定数\(C=0\)の場合です。
この場合、原始関数は\(y= \frac{1}{2}x^2\)ですね。
ではここで、元の関数\(y=x\)と原始関数\(y= \frac{1}{2}x^2\)との関係を図示してみましょう。
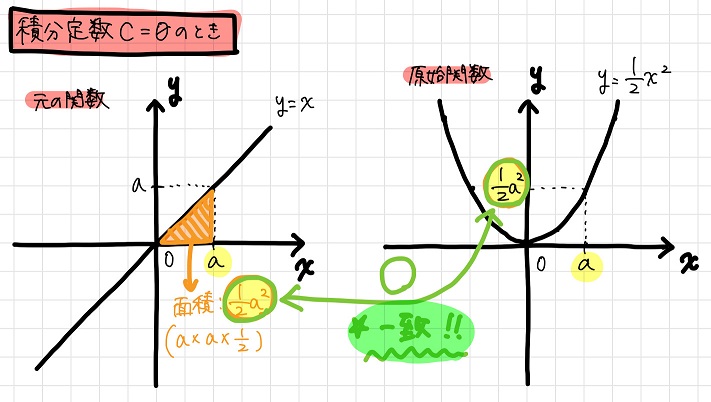
上の図より、積分定数\(C=0\)の場合、
「\(x=a\)における原始関数の値(\(\frac{1}{2}a^2\))がそのまま\(y=x\)の\(0≦x≦a\)領域の面積に対応している」
ことが分かりますね。
面積 = \(\frac{1}{2} * a * a = \frac{1}{2}a^2\)
こんな風に簡単に面積が計算できるならわざわざ定積分なんてしなくていいじゃん・・・と思われるかと思いますが、簡単な関数の方が説明が分かりやすいので、今回は元の関数をy=xとして説明しています。
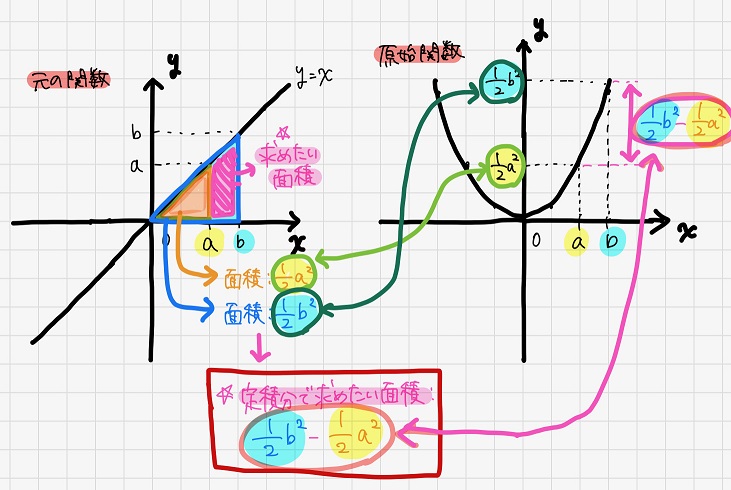
もちろん、\(x=b\)の場合も原始関数の値(\(\frac{1}{2}b^2\))がそのまま\(y=x\)の\(0≦x≦b\)領域の面積に対応します。
そのため、定積分で求めたい領域(\(a≦x≦b\))の面積は、当然
\(\frac{1}{2}b^2\)-\(\frac{1}{2}a^2\)
となります。
検討:積分定数\(C=-1\)の場合
では次に、積分定数\(C=-1\)の場合について検討してみましょう。
この場合、原始関数は\(y= \frac{1}{2}x^2 – 1\)ですね。
ここで、\(C=0\)の場合と同じように元の関数\(y=x\)と原始関数\(y= \frac{1}{2}x^2 – 1\)との関係を図示してみましょう。
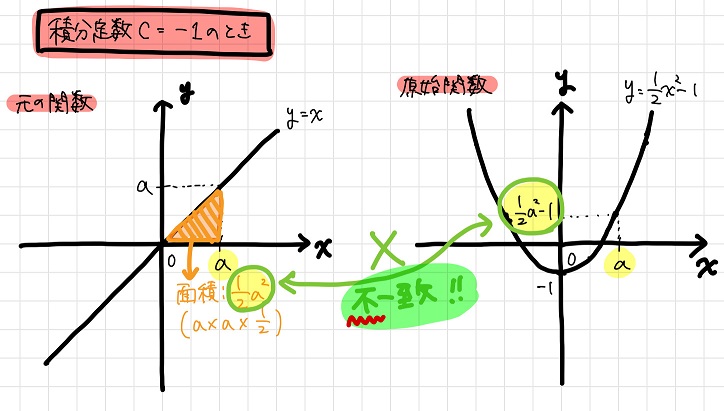
おや??どうしたことでしょう。
積分定数\(C=-1\)の場合は、
\(x=a\)における原始関数の値(\(\frac{1}{2}a^2 – 1\))は\(y=x\)の\(0≦x≦a\)領域の面積(\(\frac{1}{2}a^2\))とは異なりますね。
つまりこの場合、
元の関数\(y=x\)の面積計算を\(x=0\)から開始させるという条件では、元の関数の面積と原始関数が表す面積との整合性がとれない
ということになります。
ではここで、\(y=x\)の面積を\(x=0\)からではなく\(x=-√2\)から計算するとすればどうでしょう。
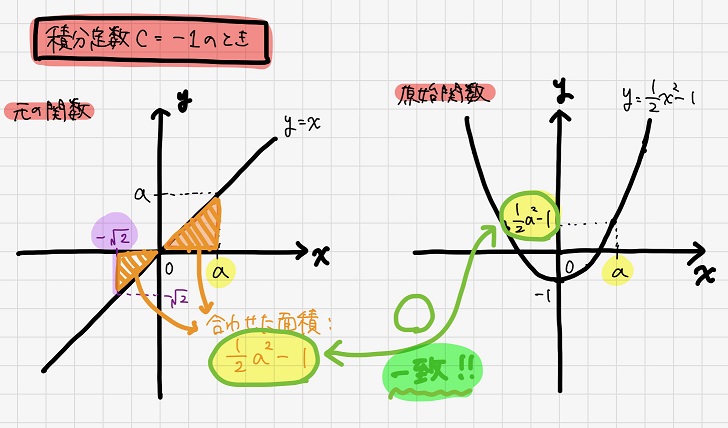
こうすれば、元の関数の面積と原始関数が表す面積との整合性がとれますね。
そのため、上の図において\(-√2≦x≦0\)の範囲の面積は負、つまり-1なのです。
つまり、
積分定数\(C\)を変化させると原始関数が表す面積(元の関数のどのxから計算した面積を表すか)が変わる
ということですね。
さて、では積分定数\(C=-1\)の場合、定積分で求めたい領域(\(a≦x≦b\))の面積はどう計算すればよいのでしょうか??
以下の図をご覧ください。
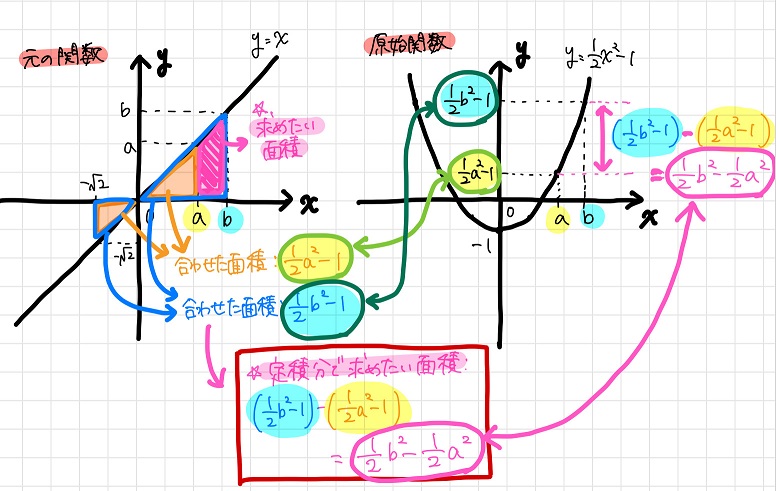
そう。実は、積分定数\(C=-1\)の場合であっても、定積分で求めたい領域(\(a≦x≦b\)の面積は
積分定数\(C=0\)の場合と同じように\(x=b\)と\(x=a\)での原始関数の差をとって計算すればよい
のです!!
差をとることで積分定数部分が消えてしまうんですね。
上の図で言うと、差をとることで\(-√2≦x≦0\)部分の面積(-1)が相殺されるってことですね。
まとめ:定積分計算に関して言えること
以上をまとめると、定積分の計算に関しては以下のことが言えることが分かりますね。
- 原始関数の積分定数Cの値により、原始関数が表す面積(元の関数のどのxから計算した面積を表すか)は変わる
- しかし原始関数が表す面積がどうであれ、定積分する範囲に関して原始関数を差し引きした結果(定積分の結果)は同じになる
↓
定積分する際には、最初から\(C=0\)として計算しても問題ない!!
これが、積分定数\(C=0\)として定積分しても問題なかった理由なのです!!
積分定数は定積分の過程で相殺されて消えるので、その値は何でもよいってことですね。
おわりに
不定積分と定積分の違いやこれらの関係性について解説した後、積分定数と定積分との関係についても解説しました。
教科書や参考書に書いてある定積分の定義式って、積分定数\(C\)が記載されてなかったりしますよね。
何で積分定数\(C\)を記載しなくても定積分が成り立つのか疑問に思っていた方(私ですが)!
今回の解説を読んで、その疑問が解決されたならば非常に嬉しく思います!
さて、微積分に関してはこれで一旦まとめを終了したいと思います。
(もしまた機会があれば、微積分の応用分野に関してまとめるかもしれませんが)
今回学習した内容を一通りまとめてみたことで、誰かに伝えるという視点で数学の内容をまとめることの難しさを身にしみて感じました。
しかし、これを続けていけば確実に自分の理解力は上がりますね。
今後は別分野に関しても、内容をまとめながら学習することを心がけていきたいと思います!
参考書籍
↓上の本の内容がもう少し詳しく説明されてます。図解が豊富で分かりやすい!コラムも面白いです。


コメントを残す